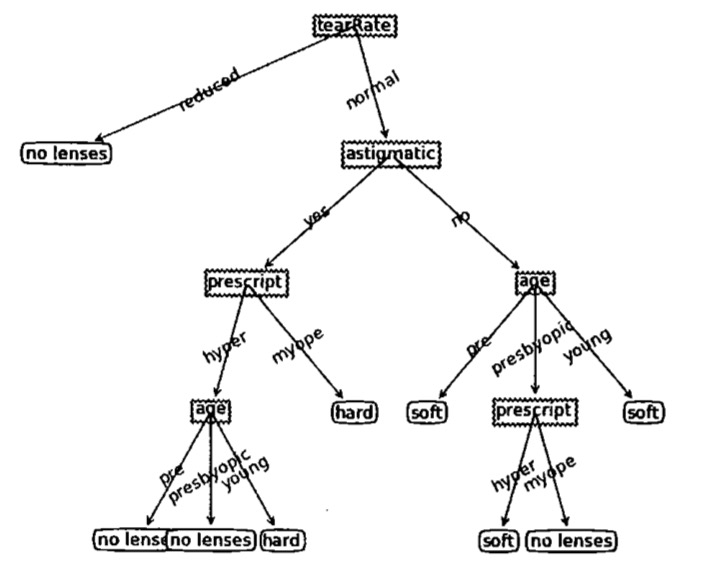
本文介绍决策树算法(Division Tree)。
决策树算法类似于用流程图进行分类判断。
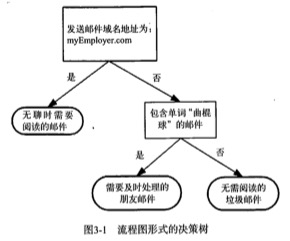
构造
- 优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据;
- 缺点:可能会产生过度匹配(overfitting)问题;
- 使用数据类型:数值型和标称型。
流程
- 收集数据:可以使用任何方法;
- 准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化;
- 分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期;
- 训练算法:构造树的数据结构;
- 测试算法:使用经验树计算错误率;
- 使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
信息增益
信息增益(Infomation Gain):在划分数据集之前之后信息发生的变化。
熵(Entropy)/香农熵:集合信息的度量方式。
如果数据集可能划分在多个分类中,则符号$x_i$的信息定义为:
$$
l(x_i) = -log_2p(x_i)
$$
其中,$p(x_i)$是选择该分类的概率。
将所有类别,每个类别里面的所有可能值包含的信息期望值叠加,就是熵的计算方式:
$$H = -\sum_{i=1}^np(x_i)log_2p(x_i)$$
例如,数据集:
1 | [[1, 'yes'], [0, 'yes'], [1, 'no'], [0, 'no'], [0, 'no']] |
其中,熵的计算为:
1 | p('yes') = 2 / 5 //yes的概率 |
划分数据集
在选择一个数据集的特征的时候,可以通过计算每个特征值划分数据集的信息增益(通过熵衡量),越高,则代表该特征值的划分效果越好。
1 | def splitDataSet(dataSet, axis, value): |
例如,对于数据集:
| 不浮出水面是否可以生存 | 是否有脚蹼 | 属于鱼类 |
|---|---|---|
| 是 | 是 | 是 |
| 是 | 是 | 是 |
| 是 | 否 | 否 |
| 否 | 是 | 否 |
| 否 | 是 | 否 |
抽象成:
1 | [[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] |
带入上述代码,结果为:
1 | 0 |
意外着,通过第一列的特征去进行分类,效果是最好的。
递归
得到原始数据集后,基于最好的特征值分类,第一次划分后,可以进行递归,每次都在剩下的特征值中取最好的进行分类,直到递归结束。
递归结束的条件是:
- 程序遍历完所有划分数据集的属性;
- 每个分支下的所有实例都具有相同的分类。
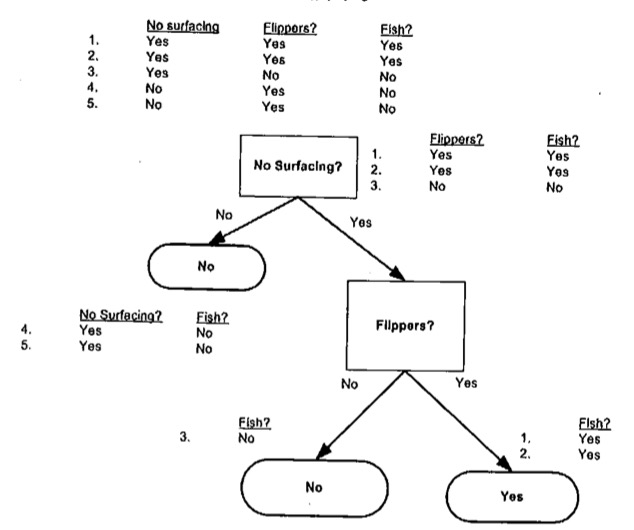
如果数据集已经处理了所有属性,但是类标签依然不是唯一的,此时可以采用多数表决的方法处理。
1 | def majorityCnt(classList): |
递归构造树:
1 | def createTree(dataSet, labels): |
结果:
1 | {'no surfacing':{0:'no', 1:{'flippers':{0:'no', 1:'yes'}}}} |
测试
1 | def classify(inputTree, featLabels, testVec): |
结果:
1 | labels:{'no surfacing', 'flippers'} |
存储
构造决策树是很耗时的任务,可以将已经构造好的树,序列化到硬盘中,要用时,在反序列化到内存中。
优化
对于某些情景,可能匹配选项太多了,会导致过度匹配(overfitting)问题,例如下图,对于这种情况,可以对其进行裁剪,去掉一些不必要的叶子节点。如果叶子节点只能增加少许信息,则可以删除该节点,将它并入到其他叶子节点中。