Word Vectors 词向量
词义
定义
传统的语言学认为:
意符 (Signifier) 和意指 (Signified) 可以互相推出。
检测
WordNet 是一个人工管理的词义库,可以用其来检测上下位 (is - a) 关系和近义词:

但是这种离散的呈现方式,有很多问题:
- 无法区分一些细微的区别,例如:adept,expert,good,practiced,proficient,skillful;
- 需要人力进行维持,并无法一直保持更新;
- 属于主观的判断;
- 很难准确计算单次的相似性。
离散的表示方式
绝大多数这种基于规则和统计的 NLP 方法将单词识别成单个原子(不可分割)的符号,例如 hotel, conference, walk。这样的方式,在向量空间里面,是类似以下的表示:

这种离散的表示方式 (Distributed Representations) ,称为 “one-hot”, 这会导致词库文件非常大。另外,其无法检测相似性。
例如,当我们输入 “Seattle motel” 时,我们其实是想搜索 “Seattle hotel”,然而,”motel” 与 “hotel” 的向量表示方式为:

两者是正交的。
基于离散相似性的表示方式
基于离散相似性的表示方式 (Distributional Similarity based Representations) 指的是结合上下文,进行语义的理解。

将词义定义成向量,再通过向量来对上下文的其他单词进行预测,从而达到理解的目的。

词嵌入的学习神经网络
我们定义好一个模型,用于预测一个单词 $w_t$ 的上下文单词的概率为:
$$p(context|w_t)=…$$
同时,定义好其错误率函数,例如:
$$J = 1 - p(w_{-t}|w_t)$$
这里的, $w_{-t}$ 代表除了 $w_t$ 以外的所有单词。
那么, 我们的目标在于,在一个大的语言集中,检索非常多 t 的位置,并调整单词的向量表示方式,来最小化错误率。
Word2vec
定义
Word2vec 可以预测每个单词的上下文词汇的概率。
两个算法,SG(Skip-grams) 和 CBOW(Continuous Bag of Words)。
两个训练方法,Hierarchical Softmax 和 Negative Sampling。
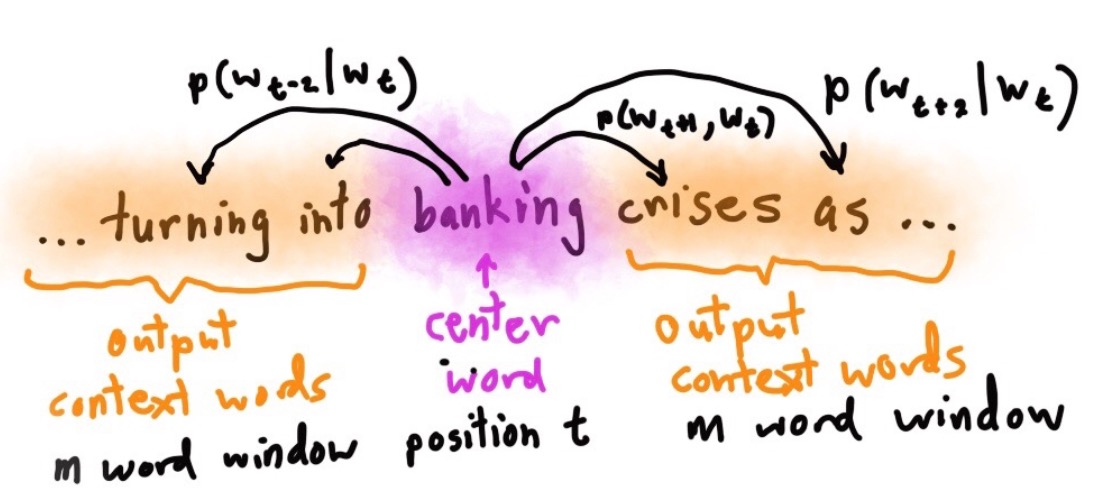
Skip-grams
对于任一个单词 $t = 1 … T$ ,建立一个半径为 $m$ 的窗口,预测该窗口中每个单词的出现概率,然后,我们尽可能地通过不断尝试单词的向量表示的方式,来最大化其概率分布。
函数(Objective/Loss/Cost Funtion)为:
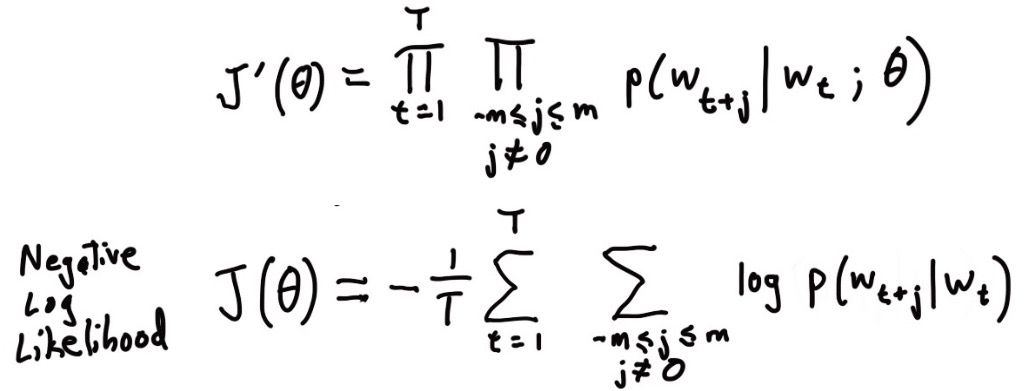
其中,$θ$ 代表要优化的变量,即是向量表示方式,下方是对数的表示方式,”-“ 号代表将最大转换成最小,这是机器学习比较喜欢的表达方式,例如错误率越低越好。
Softmax 函数
Softmax 函数用于将 $R^v$ 空间映射成概率分布:
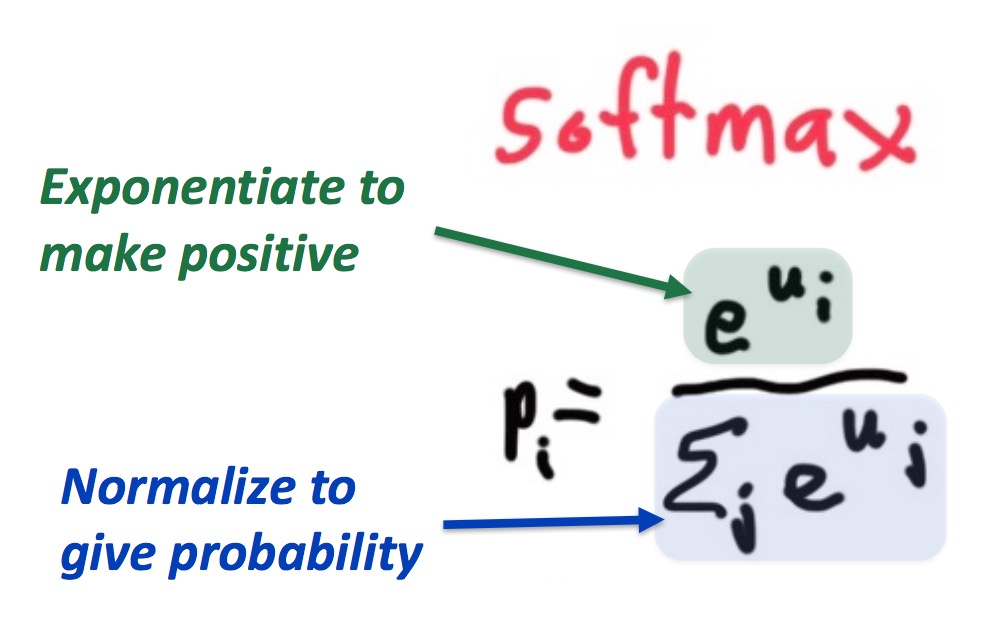
好处在于,通过幂函数,让结果变成正数,另外,让结果控制在 $[0, 1]$ 之间,实现正则化。另外,通过 $e$ 的幂函数,实现两极化,正样本的结果趋向于 $1$, 而负样本的结果趋向于 $0$。
点积
点积(Dot Product)可用于计算两个向量的相似性。
例如,向量 $u$ 和 $v$:
$$u^Tv = u.v = \sum_{i=1}^nu_iv_i$$
Word2Vec
结合 Softmax 函数和点积函数,可以预测出每个单词的半径为 $m$ 的窗口的上下文单词的出现概率。
例如,对于 $p(w_{t+j}|w_t)$ ,最简单的公式为:
$$p(o|c) = \frac{exp(u_o^Tv_c)}{\sum_{w=1}^vexp(u_w^Tv_c)}$$
其中,$o$ 代表上下文单词的索引,$c$ 代表关键字单词的索引,$v_c$ 和 $u_o$ 分别代表其向量。
为了计算方便,每个单词维持两个向量,一个是其本身的表示向量,另一个是上下文向量。
用图来表示 SG 算法如下:
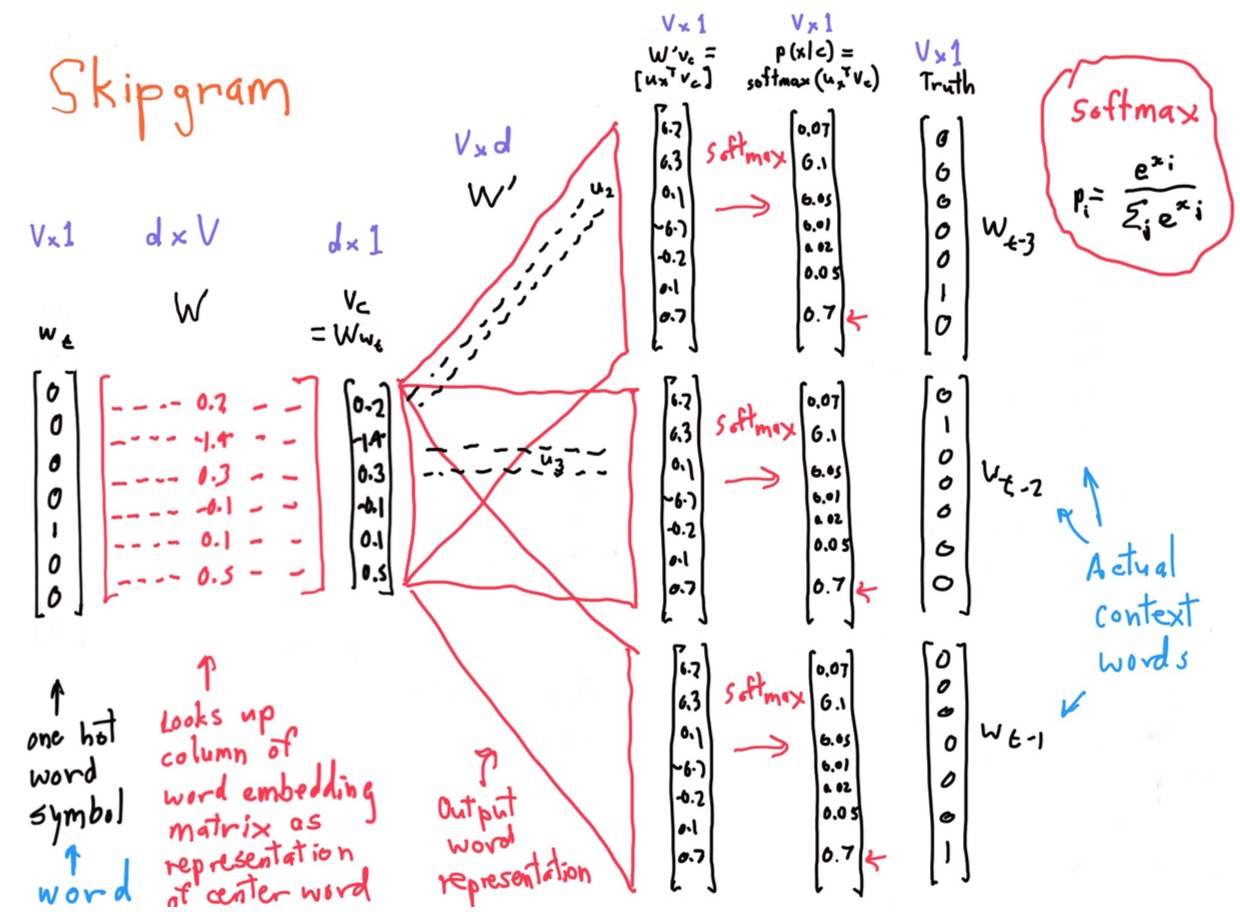
最后,通过计算 Softmax 结果与真实位置的单词向量比较,看其错误率,并进行参数调优。
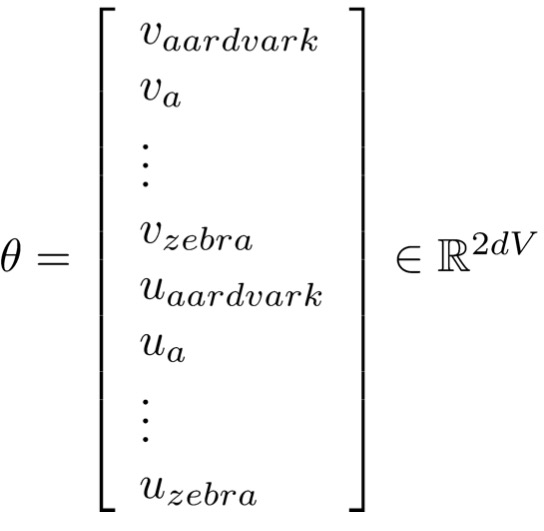
我们将所有参数的集合定义为一个长向量 $θ$ ,如果在一个 $d$ 维的向量空间中,有 $V$ 个单词,则: