ECDSA 椭圆曲线数字签名算法
签名定义
签名跟加密不同,签名只为了验证,对内容不做隐藏,为了计算方便,一般对内容的摘要(例如:压缩后的MD5)进行签名。
椭圆曲线
参考之前的文章 BlockChain-ECC 椭圆曲线
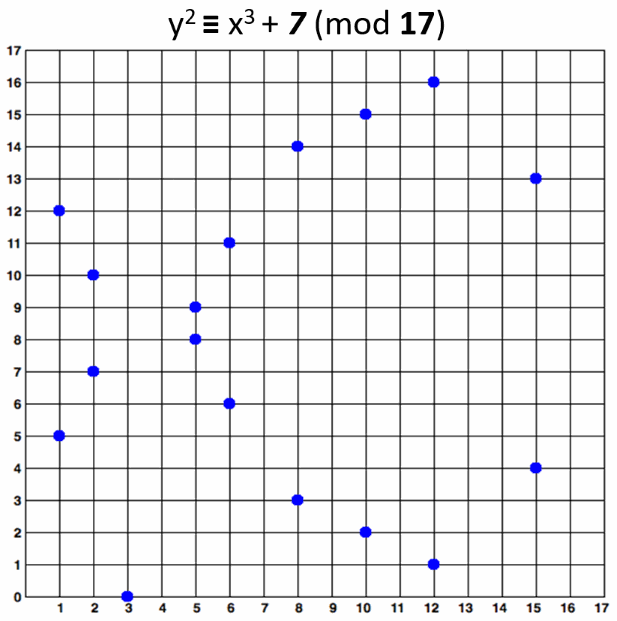
区块链用的椭圆曲线 Secp256k1
曲线方程:y² = x³ + 7

数字签名算法
椭圆公式
y^2 = (x ^ 3 + a * x + b ) mod P
参数
P: >3的质数,由于椭圆曲线是无限大实数集,为了计算方便,只取x, y 都在(0, P)内的整数点(有限域)
N: 满足上面P条件的所有点的数量(包括无限远的那个元点0)
n: 子群的点数量,称为子群的阶,一般=N
h: 子群的余因子,其实就是 = N / n,一般=1
G: 基点
a, b: 公式里的a, b
计算逆模
逆模定义:A X ≅ 1 (mod M) ,有 ((A % M) * (X % M)) % M == 1,则 A 跟 X 互为逆模
利用扩展的欧几里得算法(GCD)来计算逆模
原理:
1 | 定义 Ax + My = gcd(x, M) |
计算:
1 | ax + by = gcd(a, b) |
代码:
1 | def gcd(a, b): |
计算点加法
计算斜率
两点不同:斜率 k = [(A.y - B.y)/ (A.x - B.x )] mod P = [(A.y - B.y)% P * (A.x - B.x ) 逆] % P
两点相同:斜率 k = [(3 * A.x ^ 2 + a * A.x)/ (2 * A.y) ] mod P = [(3 A.x ^ 2 + a \ A.x)% P * (2 * A.y)逆 ] % P
计算交点
韦达定理
x = (k ^ 2 - A.x - B.x) % P
y = (-k *(x - A.x) - A.y) % P
计算点乘法
乘法本质上是加法,但是如果乘法次数太大,那么需要进行快速运算,用倍加算法拆成2的幂次方,然后再做加法
例如: 151 = 2^7 + 2 ^ 4 + 2^ 2 + 2 ^ 1 + 2 ^ 0
代码:
1 | def multi(p, count): |
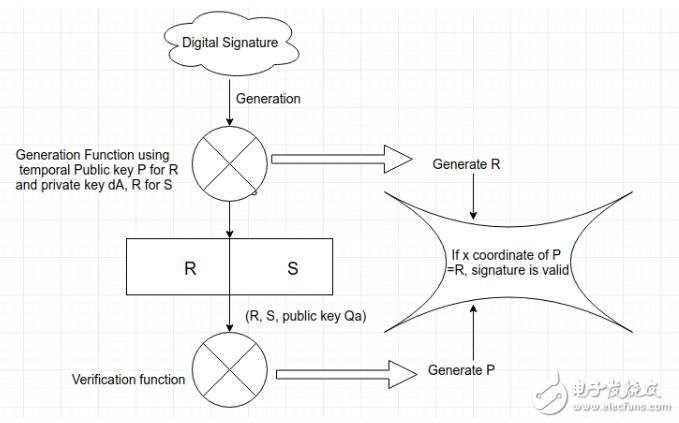
签名流程
生成密钥对
私钥 Pri:生成 < N 的随机整数
公钥 Pub:基点 G 经过 Pri 次乘法后的点(x, y)
加密内容信息
加密内容信息 m:对内容信息进行(一次或者多次)哈希处理,例如sha256,转成整数
签名
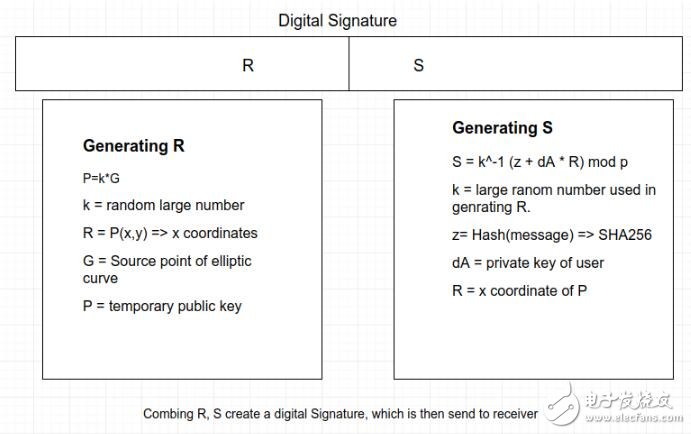
生成随机数k
生成 < N 的随机整数
计算点 R
基点 G 经过 k 次乘法后的点(x,y),验证 R 不为无穷元点 0,且 R.x 不为零
计算 s
s = [(m + R.x * Pri) / k] mod N = [(m + R.x * Pri) % N * k逆 ]% N
要验证 s 不为零,否则重新生成 k
计算 v
因为签名只传递 R.x,而不是完整的 R 坐标,R.y 可以通过 R.x 算出来,但是有多个 R.y 可能,所以需要标志位 recid
v = recovery_id + 27
其中:
R.x < N 且 R.y 是偶数: recovery_id := 0
R.x < N 且 R.y 是奇数: recovery_id := 1
R.x > N 且 R.y 是偶数: recovery_id := 2
R.x > N 且 R.y 是奇数: recovery_id := 3
签名返回值
返回 (r = R.x, s, v)元组
校验流程

计算点 P
P = (m * G + r * Pub ) / s = (m 点乘 G * s逆) 点加 (r 点乘 Pub * s逆)
判断 P.x 和 r
判断 p.x == r
总结
整体流程图: